|
Общая схема вероятностной поточной шифрсистемы
Д.Н. Колегов
Опубликовано: dl, 29.05.06 04:25
Дается общее определение вероятностной поточной шифрсистемы, охватывающее все известные шифрсистемы этого класса. Приводятся примеры новых таких шифрсистем, построенных по данному определению. Обсуждается возможность построения таким образом стойких шифрсистем с нестойкими компонентами.
Ключевые слова: шифрсистема, поточная шифрсистема, вероятностная шифрсистема, стойкость
Введение
Все шифрсистемы можно разделить на два класса - вероятностные и детерминированные. В первых результат шифрования зависит не только от ключа шифрования и открытого текста, как во вторых, но и от некоторого случайного элемента - рандомизатора. Среди современных шифрсистем большинство являются детерминированными и только единицы вероятностными. Вместе с тем известно, что внесение элемента случайности в процесс шифрования позволяет получить следующие важнейшие свойства шифрсистемы [1, 2, 3]:
- увеличивается сложность проведения атак на основе выявления статистических закономерностей функции шифрования;
- одному и тому же открытому тексту, зашифрованному на одном и том же ключе, может соответствовать много различных шифртекстов, что делает неэффективной атаку по словарю;
- увеличивается сложность проведения атак с известным открытым текстом, так как криптоаналитик может быть ограничен в необходимом количестве открытого текста (зашифрованного на одном ключе) для успешной реализации атаки;
- появляется дополнительный параметр безопасности, изменяя который можно управлять стойкостью схемы, появляется возможность увеличения времени жизни ключа.
К недостаткам вероятностного шифрования следует отнести увеличение длины шифртекста по сравнению с длиной исходного открытого текста и уменьшение скорости шифрования.
В настоящее время на практике в качестве вероятностных поточных шифрсистем широко используются поточные режимы блочных шифров [1], в которых рандомизация шифртекста достигается за счет случайного выбора векторов инициализации, называемых также синхропосылками, и передачи их, как правило, в открытом виде вместе с криптограммой открытого текста. Другим методом рандомизации шифртекста в блочных алгоритмах является добавление в открытый текст наборов случайных букв с последующим шифрованием преобразованного текста [1,2].
В настоящей работе предпринимается попытка дать общее определение вероятностной поточной шифрсистемы, под которое подпадают все известные по литературе шифрсистемы этого класса. Следуя данному определению, можно построить много новых вероятностных поточных шифросистем. Некоторые примеры таких шифрсистем приводятся. Обсуждается также возможность построения стойких вероятностных поточных шифрсистем с нестойкими компонентами.
Под шифром всюду далее понимается любой набор из пяти объектов 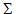 = (X, K, Y, E, D), где X, K, Y - множества соответственно сообщений (открытых текстов), ключей, криптограмм (шифртекстов), E и D - функции, E: K × X = (X, K, Y, E, D), где X, K, Y - множества соответственно сообщений (открытых текстов), ключей, криптограмм (шифртекстов), E и D - функции, E: K × X 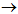 Y, D: K × Y Y, D: K × Y 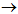 X, связанные соотношением обратимости E(k, x) = y X, связанные соотношением обратимости E(k, x) = y 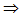 D(k, y) = x для всех x D(k, y) = x для всех x  X и y X и y  Y и называемые функциями шифрования и расшифрования соответственно. Предполагается, что сообщения, ключи, криптограммы и рандомизаторы являются словами в некоторых алфавитах. Алфавит слов в некотором множестве V обозначается AV. Предполагается также, что всякий ключ k в K представляется парой взаимозависимых ключей k1, k2 так, что k = (k1, k2), где k1 является ключом шифрования: y = E(k, x) = E(k1, x), а k2 - ключом расшифрования: D(k, y) = D(k2, y) = x. В случае, если k2 вычисляется по k1 трудно (с экспоненциальной сложностью), то Y и называемые функциями шифрования и расшифрования соответственно. Предполагается, что сообщения, ключи, криптограммы и рандомизаторы являются словами в некоторых алфавитах. Алфавит слов в некотором множестве V обозначается AV. Предполагается также, что всякий ключ k в K представляется парой взаимозависимых ключей k1, k2 так, что k = (k1, k2), где k1 является ключом шифрования: y = E(k, x) = E(k1, x), а k2 - ключом расшифрования: D(k, y) = D(k2, y) = x. В случае, если k2 вычисляется по k1 трудно (с экспоненциальной сложностью), то  называется шифром с открытым ключом, в противном случае - шифром с закрытым ключом. называется шифром с открытым ключом, в противном случае - шифром с закрытым ключом.
Определение вероятностной поточной шифрсистемы PSC
Схематически вероятностная поточная шифрсистема (PSC) изображена на рис. 1.
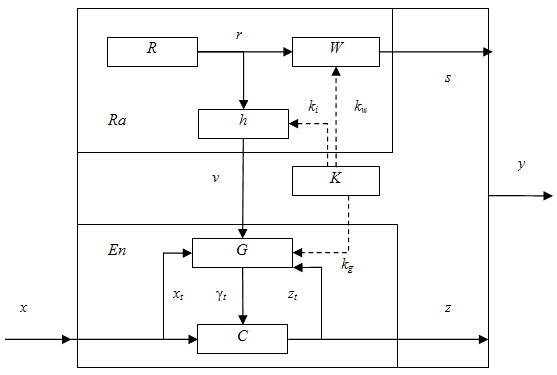
Рис. 1. Схема вероятностной поточной шифрсистемы PSC
Она состоит из ключевой системы K и блоков рандомизации Ra и шифрования En. Состав ключевой системы здесь не раскрывается, ее функция заключается в выработке тройки ключей ki 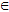 Ki, kw Ki, kw 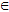 Kw и kg Kw и kg 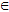 Kg, называемых ключами соответственно инициализации, свидетельства и генератора. Блок рандомизации состоит из источника (множества) рандомизаторов R и узлов свидетельства W и инициализации h. Формально узел свидетельства является некоторым шифром W = (R, Kw, S, e', d'). Он предназначен для создания свидетельства s = e'(r, kw) Kg, называемых ключами соответственно инициализации, свидетельства и генератора. Блок рандомизации состоит из источника (множества) рандомизаторов R и узлов свидетельства W и инициализации h. Формально узел свидетельства является некоторым шифром W = (R, Kw, S, e', d'). Он предназначен для создания свидетельства s = e'(r, kw) 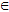 S рандомизатора r S рандомизатора r 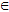 R в зависимости от ключа свидетельства kw. Формально узел инициализации является некоторой функцией h: R × Ki R в зависимости от ключа свидетельства kw. Формально узел инициализации является некоторой функцией h: R × Ki 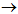 AX × AZ × Q. Он создает для блока шифрования вектор инициализации v = (x0, z0, q0) = h(r, ki). Блок шифрования состоит из генератора ключевых потоков G, представляющего собой множество конечных автоматов Mk = (AX × AZ, Q, Г, AX × AZ × Q. Он создает для блока шифрования вектор инициализации v = (x0, z0, q0) = h(r, ki). Блок шифрования состоит из генератора ключевых потоков G, представляющего собой множество конечных автоматов Mk = (AX × AZ, Q, Г, 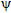 k, k, 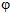 k), k k), k 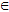 Kg, с входным алфавитом AX × AZ, выходным алфавитом Г, множеством состояний Q и функциями переходов и выходов соответственно Kg, с входным алфавитом AX × AZ, выходным алфавитом Г, множеством состояний Q и функциями переходов и выходов соответственно 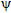 k: (AX × AZ) × Q k: (AX × AZ) × Q 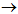 Q и Q и 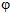 k: (AX × AZ) × Q k: (AX × AZ) × Q  Г, и шифра C = (AX, AZ, Г, e, d). Г, и шифра C = (AX, AZ, Г, e, d).
При фиксированных ключах ki, kw и k = kg шифрсистема PSC на стороне отправителя открытый текст x = x1 ... xl 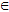 X преобразует в шифртекст z = z1 ... zl X преобразует в шифртекст z = z1 ... zl 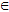 Z следующим образом: выбирается случайно рандомизатор r Z следующим образом: выбирается случайно рандомизатор r 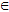 R, вычисляются его свидетельство s = e'(r, kw), вектор инициализации (x0, z0, q0) = h(r, ki), ключевой поток R, вычисляются его свидетельство s = e'(r, kw), вектор инициализации (x0, z0, q0) = h(r, ki), ключевой поток 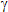 = = 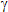 1 ... 1 ... 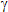 l, где для любого t = 1, ..., l l, где для любого t = 1, ..., l
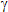 t = t = 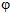 k((xt-1, zt-1), qt), qt = k((xt-1, zt-1), qt), qt = 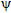 k((xt-1, zt-1), qt-1) и zt = e( k((xt-1, zt-1), qt-1) и zt = e(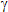 t, xt). t, xt).
Пара (s, z) передается в канал связи. На стороне получателя шифрсистема PSC восстанавливает открытый текст, вычисляя последовательно r = d'(s, kw), (x0, z0, q0) = h(r, ki) и для t = 1, ..., l
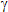 t = t = 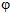 k((xt-1, zt-1), qt), qt = k((xt-1, zt-1), qt), qt = 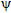 k((xt-1, zt-1), qt-1) и xt = d( k((xt-1, zt-1), qt-1) и xt = d(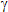 t, zt). t, zt).
Классификация шифрсистем PSC
PSC называется шифрсистемой с открытым рандомизатором, если e'(r, kt) = r для всех kw 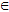 Kw. Она называется шифрсистемой с закрытым рандомизатором, если при неизвестном ключе kw значение рандомизатора r трудно вычислимо по его свидетельству s = e'(r, kw). PSC называется шифрсистемой с открытым или закрытым ключом, если соответственно таковым является шифр W в ней. Она называется синхронной, если все автоматы Mk в G автономные: их функции Kw. Она называется шифрсистемой с закрытым рандомизатором, если при неизвестном ключе kw значение рандомизатора r трудно вычислимо по его свидетельству s = e'(r, kw). PSC называется шифрсистемой с открытым или закрытым ключом, если соответственно таковым является шифр W в ней. Она называется синхронной, если все автоматы Mk в G автономные: их функции 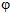 k((x, z), q) и k((x, z), q) и 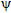 k((x, z), q) зависят от (x, z) фиктивно, т.е. являются по существу функциями только от q. В этом случае, естественно, считается, что значения функции h лежат в Q, т.е. h: R × Ki k((x, z), q) зависят от (x, z) фиктивно, т.е. являются по существу функциями только от q. В этом случае, естественно, считается, что значения функции h лежат в Q, т.е. h: R × Ki 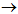 Q. PSC называется шифрсистемой с закрытым вектором инициализации, если при неизвестном ключе ki значение h(r, ki) трудно вычислимо по рандомизатору r. Она называется шифрсистемой с тождественной инициализацией, если h(r, ki) = r для всех ki Q. PSC называется шифрсистемой с закрытым вектором инициализации, если при неизвестном ключе ki значение h(r, ki) трудно вычислимо по рандомизатору r. Она называется шифрсистемой с тождественной инициализацией, если h(r, ki) = r для всех ki  Ki. Ki.
Примеры шифрсистем PSC
Многочисленные примеры шифрсистемы PSC различных типов можно получить, выбирая в ней различными способами компоненты W, G, C, h, K, R. Например, при подходящих h, K, R в качестве (W, G, C) в PSC могут выступать комбинации: (AES, RC4, + mod 256), (RSA, BBS, ), (RSA, RSA, 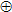 ), ( ), (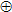 , LFSR+filter, , LFSR+filter, 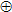 ) и другие [4]. Примером шифрсистемы PSC с закрытым вектором инициализации может служить PSC, в которой ключом ki служит многочлен f(x) над конечным полем, обновляемый после зашифрования не более n-1 открытых текстов, где n - степень f, и h(r, ki) = f(r). В других PSC с закрытым вектором инициализации в роли h могут использоваться различные ключевые хэш-функции. Примерами шифрсистем с тождественной инициализацией являются блочные шифры в режиме поточного шифрования, а также синхронные поточные шифры, построенные на основе генераторов ключевого потока с функциональными блоками в качестве закрытого ключа. ) и другие [4]. Примером шифрсистемы PSC с закрытым вектором инициализации может служить PSC, в которой ключом ki служит многочлен f(x) над конечным полем, обновляемый после зашифрования не более n-1 открытых текстов, где n - степень f, и h(r, ki) = f(r). В других PSC с закрытым вектором инициализации в роли h могут использоваться различные ключевые хэш-функции. Примерами шифрсистем с тождественной инициализацией являются блочные шифры в режиме поточного шифрования, а также синхронные поточные шифры, построенные на основе генераторов ключевого потока с функциональными блоками в качестве закрытого ключа.
Стойкие шифрсистемы PSC с нестойкими компонентами
Понимая под стойкостью вычислительную стойкость к атакам с известным открытым текстом с целью определения неизвестного ключа, рассмотрим шифрсистему PSC в предположении, что требованию стойкости удовлетворяет лишь некоторые из ее компонент. Так, если стоек генератор в G, то криптоаналитик, зная x, s, z и, следовательно, ключевой поток на выходе генератора, не сможет вычислить вектор инициализации. В отсутствие последнего он не может знать рандомизатора и, следовательно, не может провести ни атаку на R (с целью предсказания следующего рандомизатора), ни атаку с известным открытым текстом на W. Если же стойкими являются шифр W и источник рандомизаторов R, то можно допустить нестойкий генератор G. То же самое возможно в случае односторонней функции h.
Литература
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. - М.: Издательство ТРИУМФ, 2003.
- Асосков А.В., Иванов М.А., Мирский А.А., Рузин А.В., Сланин А.В., Тютвин А.Н. Поточные шифры. - М.: КУДИЦ-ОБРАЗ, 2003. - 336 с.
- Молдовян. Скоростные блочные шифры. - СПб.: Издательство БХВ-Петербург, 2002.
- Агибалов Г.П. Вероятностные схемы симметричного поточного шифрования над конечным полем // Вестник Томского государственного университета. Приложение. - 2005. - N 14 - С. 39 - 42.
|
 |




